Le calcul différentiel pour l'IA

By Paul Claret

5 minutes read - 01/12/24

Le calcul différentiel est essentiel dans de nombreuses applications de l'intelligence artificielle, notamment dans l'optimisation des réseaux neuronaux (descente de gradient). Ce cours est conçu pour couvrir uniquement les bases nécessaires à une compréhension des algorithmes d'optimisation en IA. Nous ne couvrirons pas les concepts avancés comme les équations différentielles ou les théorèmes complexes, mais vous serez en mesure de suivre l'intégralité des cours sur l'IA avec ces notions de base.

Comme pour l’algèbre linéaire, si vous êtes déjà familier avec ces concepts, n’hésitez pas à passer à la section suivante.

Définition du calcul différentiel

Le calcul différentiel est la branche des mathématiques qui étudie les variations locales des fonctions, notamment grâce aux concepts de dérivée et de gradient.
Dans le contexte de l’IA, il est principalement utilisé pour :

Analyser la sensibilité d'une fonction (comment une petite variation de l'entrée affecte la sortie).
Optimiser les modèles via des algorithmes tels que la descente de gradient.

Dérivée d’une fonction

Définition intuitive

La dérivée mesure le taux de variation d'une fonction. Si une fonction $f (x)$ représente une courbe, sa dérivée $f^{'} (x)$ représente la pente de cette courbe en un point donné.

Je doute que j'ai besoin de ré-expliquer cela mais voici un example avec la fonction carrée:

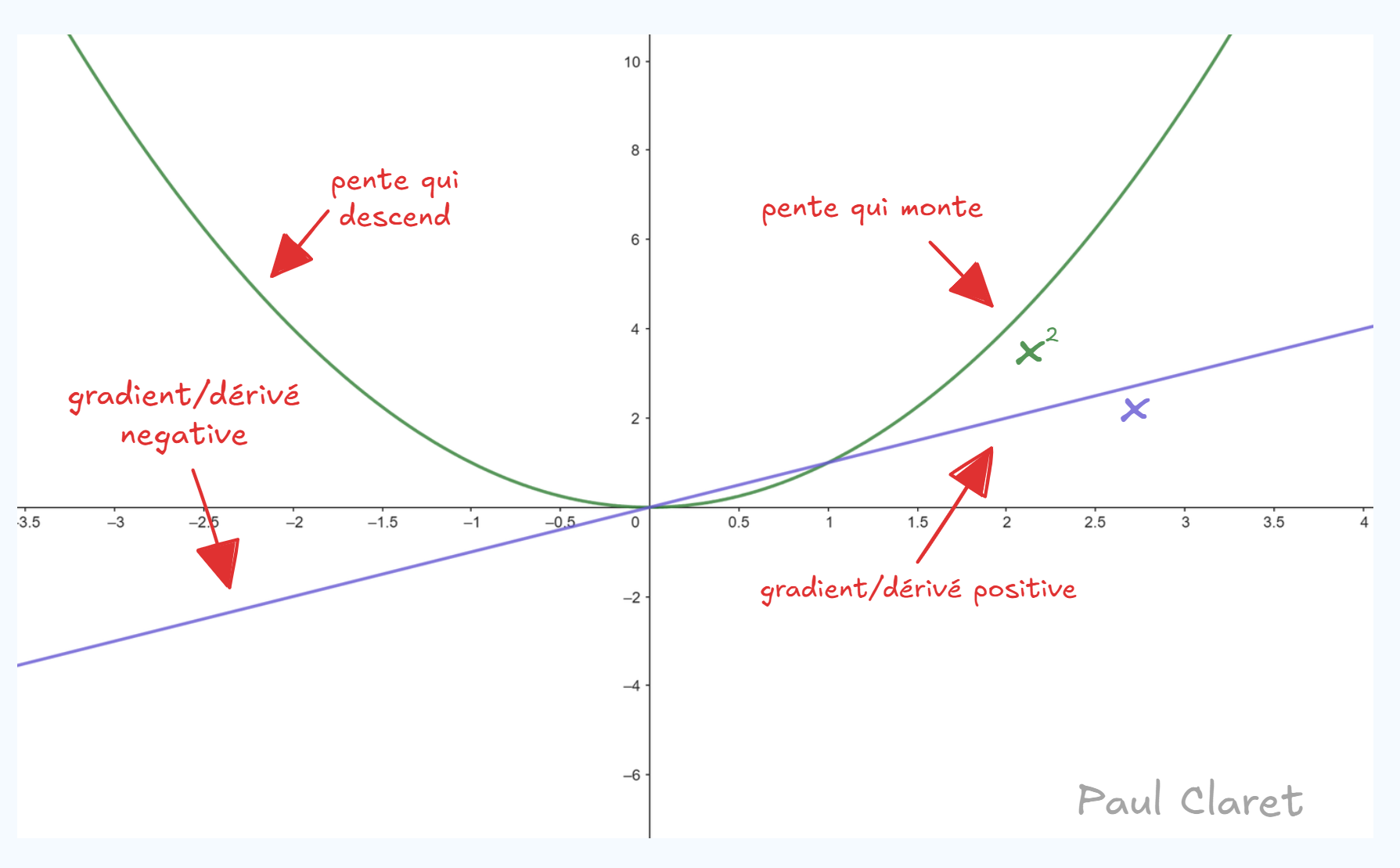
Calcul différentiel pour l'IA explication

Exemple :

Cela signifie que pour une petite variation $Δ x$ autour d’un point $x$ , la variation de $f (x)$ est approximée par :

Notation et calcul pratique

Forme	Notation	Exemple
Dérivée simple	$f^{'} (x)$ ou $\frac{df}{d x}$	Si $f (x) = 3 x^{3}$ , alors $f^{'} (x) = 9 x^{2}$
Dérivée partielle	$\frac{\partial f}{\partial x}$	Pour $f (x, y) = x^{2} + y^{3}$ , $\frac{\partial f}{\partial x} = 2 x$
Gradient (fonction multivariée)	$\nabla f$	$\nabla f (x, y) = [\frac{\partial f}{\partial x} \frac{\partial f}{\partial y}]$

Quelques règles pratiques

1. Règle de la somme

Si $f (x) = g (x) + h (x)$ , alors $f^{'} (x) = g^{'} (x) + h^{'} (x)$

2. Règle du produit

Si $f (x) = g (x) \cdot h (x)$ , alors : $f^{'} (x) = g^{'} (x) h (x) + h^{'} (x) g (x)$

3. Règle du quotient

Si $f (x) = \frac{g ( x )}{h ( x )}$ , alors : $f^{'} (x) = \frac{g ^{'} ( x ) h ( x ) - h ^{'} ( x ) g ( x )}{( h ( x ) ) ^{2}}$

4. Règle de la chaîne (Chain Rule)

Essentielle pour les réseaux neuronaux :
Si $f (x) = g (h (x))$ , alors $f^{'} (x) = g^{'} (h (x)) \cdot h^{'} (x)$ .

Exemple pratiques

Applications en IA : Descente de gradient

La dérivée est au cœur des algorithmes d’optimisation. L'optimisation est le fait d'ajuster les poids pour que notre model soit plus précis. Pour cela, on utilise des algorithmes qui calcul dans quel sens, les poids devraient aller. Augmenter ou Diminuer. Voir mon article sur le gradient. Le gradient nous donne donc une indication sur comment ajuster nos poids pour notre model.

Exemple simple :

Si nous avons une fonction de perte $L (w)$ (mesurant l’erreur d’un modèle), l’objectif est de trouver les paramètres $w$ qui minimisent cette fonction.

La mise à jour des paramètres suit la règle :

où $η$ est le taux d’apprentissage (learning rate).

Pour aller plus loin :

Calcul différentiel - Wikipédia

Si vous êtes avancés:

Introduction au gradient - 3Blue1Brown (vidéo YouTube)

Vous voulez apprendre l'IA en autonomie ?

Si vous êtes nouveau sur mon site, je vous invite à aller voir ma page sur Roadmap IA qui regroupe tous mes articles dans l'ordre pour vous facilitez l'apprentissage.