L'algèbre linéaire pour l'IA

By Paul Claret

5 minutes read - 03/12/24

De nombreux livres et cours ont déjà été écrits dessus. Mon cours n'a pas pour but de vous apprendre dans le détail tous les aspects de l'algèbre linéaire, mais seulement les aspects que nous allons utiliser dans ce cours.

Si vous vous intéressez au sujet et voulez aller plus loin, je vous invite à le faire, mais je voulais juste vous prévenir que nous n'allons pas parler de matrice de passages, théorèmes du rang, endomorphismes ou ce genre de choses puisqu'elles ne seront pas utilisées dans ce cours. (peut-être à l'avenir quant au fur et à mesure que j'ajoute du contenu de jours en jours, mais ce cours se veut centré sur l'IA).

Si vous connaissez déjà le contenu de ce cours de maths juste en lisant les grands titres, je vous invite à passer à la section suivante.

Définition de l'algèbre linéaire

La définition de l'algèbre linéaire est la suivante:

L’algèbre linéaire est la branche des mathématiques qui s'intéresse aux espaces vectoriels et aux transformations linéaires, formalisation générale des théories des systèmes d'équations linéaires.

Les vecteurs

Pour représenter des vecteurs (dont vous êtes probablement déjà familier), nous utilisions la notation suviante:

v = ⎝ ⎛ x y z ⎠ ⎞ o u v = (x, y, z)

En ce qui concerne les operations sur les vecteurs voici une liste pour vous les rappeler:

Opérations

Nom	Notation	Explicaiton
Commutativité de l'addition	$u + v = v + u$	Les vecteurs s'additionnent dans les deux sens
Associcivité de l'addition	$(u + v) + w = u + (v + w)$	L'ordre d'addition des vecteurs n'a as d'importance
Element neutre	$u + 0 = u$	Le vecteur nul additioné à n'importe quel vecteur $u$ donne le vecteur $u$
Opposé	$u + - u = 0$	un vecteur additioné à son opposé donne le vecteur nul
Associativité de la multiplication de deux scalaires	$k (c u) = (k c) u$
Distributivité lors de l'addition	$k (u + v) = k u + k v$
Distributivité du produit de scalaire sur l'addition	$u . (v + w) = u . v + u . w$
Associtivité des scalaires dans le produit scalaire	$k_{1} u . k_{2} v = (k_{1} k_{2}) . u . v$
Produit scalaire	$(x_{1}, x_{2}, x_{3}) . (y_{1}, y_{2}, y_{2}) = x_{1} y_{1} + x_{2} y_{2} + x_{3} y_{3}$	voir multiplication de matrice pour plus de détails
Relation de Chasles	$A B + BC = A C$	voir image ci-dessous

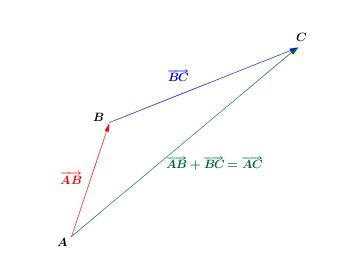
Les matrices

Les deux notations précédentes : verticales et horizontales pour les vecteurs sont correctes, mais les vecteurs peuvent aussi être vu comme des matrices de taille $R_{m . n}$ ou le $R$ indique une matrice remplie de nombres réels et les indices $m . n$ indique la taille de la matrice. Plus précisément $m$ le nombre de lignes et $n$ le nombre de colonnes.

Une matrice ne s'écrit pas avec des parenthèses mais des crochets:

A = [a c b d]

Ici j'ai défini une matrice A qui contient des nombres $a, b, c$ et $d$ . Sa taille vous l'aurez deviné est $2.2$ puisqu'elle contient 2 lignes et 2 colonnes. Vous êtes normalement capable de me donner les tailles suivantes:

A = [123] B = ⎣ ⎡ 9.2 π 7.4576812 ⎦ ⎤ C = ⎣ ⎡ a_{11} a_{21} a_{31} a_{12} a_{22} a_{32} a_{13} a_{23} a_{33} a_{14} a_{24} a_{44} ⎦ ⎤

Si vous avez dit $A_{1.3}$ ou vecteur ligne, $B_{3.1}$ ou vecteur colone et $C_{3.4}$ vous avez raison.

Vous remarquerez que pour la matrice $C$ . Je l'ai rempli de nombres a avec des indices $a_{ij}$ . Les indices $i$ et $j$ représentent respectivement les lignes et colonnes du nombre $a$ .

Si je parle de $a_{23}$ je parle du nombre se trouvant dans la ligne 2 et colonne 3 de la matrice $C$ .

Cette fois-ci, le nombre de colonnes et lignes comptent (on ne peut pas changer comme on le voulait pour les vecteur de colonne à ligne...)

Maintenant, passons aux opérations:

Opération

Addition de matrice

A = [a c b d] B = [w y x z] A + B = [a + w c + y b + x d + z]

Attention, il faut que les deux matrices soient de la même taille pour pouvoir les additionner. Sinon c'est impossible !

Multiplication par un scalaire

A = [a c b d] e t λ \in R λ . A = [λa λ c λb λ d]

Soustraction

A - B = A + (- B)

Il suffit d'utiliser les deux propriétés précédentes pour vous rendre compte que c'est une multiplication par un scalaire (-1) et une addition.

Transposition

A = [a c b d] A^{T} = [a b c d]

Simplement: les lignes devienent les colonnes et les colonnes, les lignes.

Multiplication

C'est le point le plus important ici !!!!

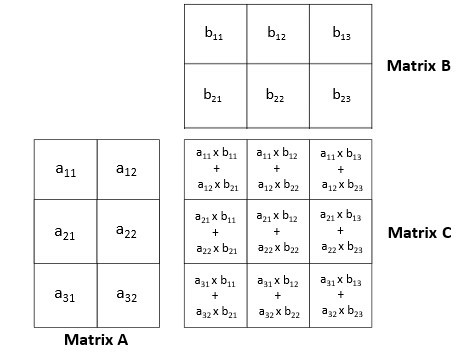
Ici c'est le produit $A B$ . Mais ce n'est pas le même pour $B A$ . La multiplication n'est pas commutative. Elle est cependant associative: $C (A B) = (CB) A$ et distributive $C (A + B) = C A + CB$ . Mais il faut cependant que les matrices que l'on multiplie soient de la bonne taille.

Qu'est-ce que j'entends par bonne taille ?

Il faut que le nombre de lignes de la première matrice soit égale au nombre de colonnes de la seconde matrice et que le nombre de colones de la première matrice soit égale au nombre de lignes de la seconde ! Si cette condition n'est pas respectée, on ne peut pas mutiplier les deux matrices.

Autrement dit:

R_{m . n} \times R_{n . m} = O K R_{m . n} \times R_{n 2. m 2} = NON

avec $n \neq = n 2$ et $m \neq = m 2$ .

Pour aller plus loin:

Ce que je vous ai présenté dans ce cours est plus que suffisant concernant le domaine de l'algèbre linéaire pour une application à l'intelligence artificielle. Comme vous allez le voir, nous n'utiliseront que les multiplications de matrice, leurs additions et quelques petits trucs et astuces supplémentaires que je vous expliquerai lors du cours approprié.

Si vous souhaitez aller plus loin, je vous invite à commencer par ces ressources. Elles sont complètes ensemble et couvrent une grande partie du domaine. Mais ce n'est pas du tout obligatoire pour la suite.

Algèbre linéaire — Wikipédia

Matrix (mathematics) - Wikipedia

https://lerasle.perso.math.cnrs.fr/docs/LinearAlgebra.pdfhttps://lerasle.perso.math.cnrs.fr/docs/LinearAlgebra.pdf

Vous voulez apprendre l'IA en autonomie ?

Si vous êtes nouveau sur mon site, je vous invite à aller voir ma page sur Roadmap IA qui regroupe tous mes articles dans l'ordre pour vous facilitez l'apprentissage.